(This post is for prospective freshmen enrolling in the Massachusetts Institute Technology. I wish I knew all this early enough, so now I'm telling it to you!)

Origami? Folding bits of paper? You mean that children's pastime? It can't possibly be of any "real" use, right?
What if I told you that origami has been applied in space technology?

The 6th International Meeting on Origami in Science, Mathematics and Education (6OSME) was held in Tokyo University in August to help origami researchers, artists and educators share their ideas on the connections between origami and a wide range of other fields, including applications in theory and industry.

Back in 2010 I tinkered around with 3D graphics, and I learned how to use OpenGL, a 3D graphics engine, with the only language I knew well, Haskell. Eager to try it out, I embarked on a project to build from scratch a molecular graphics engine, because cool images of molecules always impressed me. Below are some snapshots from the program Hmol that I wrote:

Hmol is publicly available via Github under the GNU GPLv3 License (details in the Licensing section at the bottom).

I distinctly remember finishing much of the development during my exam period—no classes and no homework, so lots of spare time!

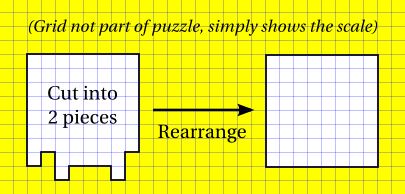
Grab a milk or juice carton and there's a fair chance you'd find that it's from Tetra Pak, a Swedish company that focuses on food packaging and processing solutions. A few months ago Tetra Pak invited ten people from around the world to a package design workshop aimed at brainstorming an improved design to one of their commercial packages. I qualified through their "Can You Fold It?" competition, in which contestants had to dream up a simple but creative way to close the end of a cardboard tube—which is basically what package manufacturers have to do.

Image from "Can You Fold It?" qualification phase

Tetra Pak's pioneering product was the Tetra Classic®, but probably more familiar is the Tetra Rex®.

One of the talks I usually give is on geometric dissections, which I begin with the following puzzle from (Lindgren 1964):

I thought it might have been more fun to give the puzzle to the prospective audience one week before I actually presented the solution, so I did that for an upcoming presentation on geometric dissections for students from Raffles Girls' School. I hope they got very frustrated by the puzzle. I also promised to give a hint to the puzzle, but I forgot to post it! Highlight the hint if you want to read it...

Lindgren, Harry (1964). Geometric Dissections.  D. Van Nostrand.

There was this thing going on Facebook:

I was given Stefan Banach (Poland). I will not discuss the Banach-Tarski Paradox.

Stefan Banach was one of the 20th century's greatest mathematicians. His self-taught prowess impressed the renowned Prof. Hugo Steinhaus, who supported Banach's career. His doctoral thesis sparked and grew into the field of "Functional Analysis", which has proved fundamental to Quantum Mechanics and Differential Equations (used widely in engineering). During World War II he and fellow academics were sheltered from Nazi persecution by employment as "lice feeders" at a Typhus Research Institute. (from Wikipedia)

He proved that:

1. Throw a world map on the floor. There's always a way to hammer a nail through the map and the floor so that the nail's position on the map exactly corresponds to its actual location.
2. Take a piece of paper, fold a paper airplane and press it flat within the original boundary of the paper. One of the points in the paper has been returned to its original position.

These are consequences of the Banach fixed-point theorem, which actually says that if we "shrink" the world (e.g. into a "map") so every pair of points can only get closer (this also happens when folding), there will be a "fixed point". The world might be (1) Earth, (2) a piece of paper or some other strange, convoluted, theoretical world.

This is one of many "fixed-point theorems", all of which say that if you take a "world", transform it so-and-so, then some point in the world must have remained immobile. The more famous Brouwer fixed-point theorem has been applied in Economics, to show that markets (the "world") have "fixed points" (e.g. balances between supply and demand).

I must thank a friend for telling me a basic form of this layman explanation many years ago; it has stuck with me all these years.

Next week I'm conducting an origami math workshop for Grade 8 students, and one of the activities will be to fold a skeletal octahedron (really simple modular origami). The students will be asked to choose between five octahedra I already folded in various colors, to see what kind of color schemes and arrangements appeal to them.  We can then discuss about symmetry, graph coloring and more.

It would also be interesting to see which color schemes people like, even before the workshop, so here goes!

If you're studying undergrad math, physics or chemistry, chances are you've heard of this thing called a "Group" that is studied in "Group Theory". What is it and why is it so important? I'll explain in a simple way.

The most familiar group is our number system; we have a bunch of numbers, and we have this thing called "$+$" which can take two numbers and churn out another number. A group is just a set of objects, and you have one "operation" (usually called "$\ast$" or "$+$", but those are just names) that tells you how to combine objects to produce other objects in that set, subject to a few rules. Why devise such a "strange chasing game" in a set of objects? That's because such systems are omnipresent in a stupendous array of phenomena:

Look behind Creation!
Exemplified in just a few given equations.
Crazy.

As part of my effort to expose myself to more art, today I attended Art Stage Singapore, which showcased more than 130 galleries' worth of art, mostly from the Asia-Pacific region. The six hours that I had weren't nearly enough for me to experience all of the art pieces there. Here's some of the pieces that I liked:

I also liked Malaysian artist Haslin Ismail's "Book Land", which cuts and assembles parts of books and other materials to form castles of fantasy and dioramas that bring the books' contents to life.