Mathematics Project Proposals
In the real world, math is about solving unsolved problems, analyzing unfamiliar situations, devising new mathematical systems and tools, exploring unknown landscapes and more — all the while reasoning with clear, rigorous logic. Students of math must ask their own questions and search for their own directions. These skills are essential outside math, but I believe that math research is a good way to train them. With proper guidance, students can potentially discover something truly original.
This page proposes math projects of various difficulties to be investigated by high school students. I try to propose unsolved questions; investigators might as well put their efforts into something actually useful. Completely solving unsolved questions may be too much to expect, but I think partial progress (e.g. only works for special cases), even by intuitive means (i.e. not perfectly rigorous) or computer programs, would already be impressive.
Top priority for any project would be a thorough literature review to check what has been analyzed and what results are known. That arms the investigator with tools developed by those in the field, avoids reinventing the wheel, and learns what the professionals consider to be promising or important. Each proposal ends with a few suggested readings if it came from existing ideas, but not if I thought it up myself. In both cases, investigators should search further on their own, and ask:
Each proposal ends with a few possible methods of attack or possible directions of inquiry, but I would prefer the investigators find their own way forward independently. Investigators who are lost or stuck can send a request for further suggestions or more advanced directions to research.queries@gmail.com. Unfortunately I cannot guarantee that my suggestions will lead anywhere at all, but in any case investigators are recommended to think beyond them.
Good luck, and I'll be glad to learn of any progress in these projects! Keep me posted, or give any feedback, through the contact form at the bottom.
This page proposes math projects of various difficulties to be investigated by high school students. I try to propose unsolved questions; investigators might as well put their efforts into something actually useful. Completely solving unsolved questions may be too much to expect, but I think partial progress (e.g. only works for special cases), even by intuitive means (i.e. not perfectly rigorous) or computer programs, would already be impressive.
Top priority for any project would be a thorough literature review to check what has been analyzed and what results are known. That arms the investigator with tools developed by those in the field, avoids reinventing the wheel, and learns what the professionals consider to be promising or important. Each proposal ends with a few suggested readings if it came from existing ideas, but not if I thought it up myself. In both cases, investigators should search further on their own, and ask:
- What has been done before?
- What can I try?
- How can I generalize this?
Each proposal ends with a few possible methods of attack or possible directions of inquiry, but I would prefer the investigators find their own way forward independently. Investigators who are lost or stuck can send a request for further suggestions or more advanced directions to research.queries@gmail.com. Unfortunately I cannot guarantee that my suggestions will lead anywhere at all, but in any case investigators are recommended to think beyond them.
Good luck, and I'll be glad to learn of any progress in these projects! Keep me posted, or give any feedback, through the contact form at the bottom.
"Good" Dissections
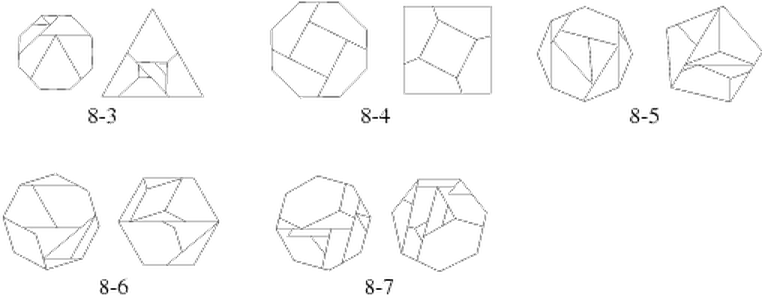
Geometric dissections concern the cutting of polygonal shapes into a finite number of pieces and rearranging the pieces into another shape. Here are some sample dissections:
Do you like some dissections more than others? What is a "good" dissection? Does it depend on the number of pieces used? Symmetry? Flipping over pieces? Does it depend on the starting and ending shapes?
Suggestions
- What criteria, or combination of criteria, for "good'' dissections can be formalized and stated using a mathematical language?
- Using those criteria, write a mathematical procedure (possibly a computer program?) that can tell if dissections are "good" or not.
- Find large, general families of "good" dissections.
- Challenging: how do we tell if a dissection uses the fewest number of pieces?
Note that the Wallace-Bolyai-Gerwien Theorem guarantees that any two polygons of equal area are equidecomposable, that is, one can be dissected and rearranged into the other.
(Frederickson, 1997) and (Lindgren, 1964) survey several types of dissections and the techniques used to generate them, as well some of the history behind these puzzles. (Frederickson, 2002) does the same for special dissections whose pieces can be hinged together. There is probably more literature on this topic that can be found.
References
(Frederickson, 1997) Greg N. Frederickson. Dissections: Plane and Fancy. Cambridge University Press (1997).
(Frederickson, 2002) Greg N. Frederickson. Hinged Dissections: Swinging and Twisting. Cambridge University Press (2002).
(Lindgren, 1964) Harry Lindgren. Geometric Dissections. Princeton, N.J.: D. Van Nostrand (1964).
(Frederickson, 2002) Greg N. Frederickson. Hinged Dissections: Swinging and Twisting. Cambridge University Press (2002).
(Lindgren, 1964) Harry Lindgren. Geometric Dissections. Princeton, N.J.: D. Van Nostrand (1964).
Dissecting Polyhedra
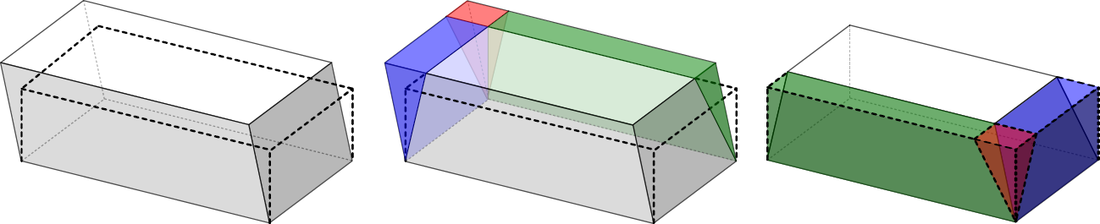
The Wallace-Bolyai-Gerwien Theorem guarantees that any two polygons of equal area are equidecomposable, that is, one can be dissected into a finite number of pieces and rearranged into the other. However, the 3D version of this doesn't work; for example, a cube is not equidecomposable with a tetrahedron of the same volume. But some dissections of polyhedra do work, such as the one illustrated below and many more described in (Frederickson, 1997) and (Frederickson, 2002). But can you find large, general families of polyhedron pairs that are equidecomposable?
Suggestions
- Are right prisms with equal base area and height equidecomposable?
- Find large, general families of polyhedron pairs that are equidecomposable.
Several techniques for creating dissections listed in (Frederickson, 1997), (Frederickson, 2002), (Lindgren, 1964) and further literature will be useful.
References
(Frederickson, 1997) Greg N. Frederickson. Dissections: Plane and Fancy. Cambridge University Press (1997).
(Frederickson, 2002) Greg N. Frederickson. Hinged Dissections: Swinging and Twisting. Cambridge University Press (2002).
(Lindgren, 1964) Harry Lindgren. Geometric Dissections. Princeton, N.J.: D. Van Nostrand (1964).
(Frederickson, 2002) Greg N. Frederickson. Hinged Dissections: Swinging and Twisting. Cambridge University Press (2002).
(Lindgren, 1964) Harry Lindgren. Geometric Dissections. Princeton, N.J.: D. Van Nostrand (1964).
Light Ray Prediction
Suppose a light ray travelling in the plane is trapped in a rectangular box whose walls are mirrors that the light bounces off against. If its speed and initial position and direction are known, how do we predict where the light would have reached after a certain amount of time has passed? Working it out seems hard at first because each bounce must take into account the wall involved, which affects the direction of the deflected light ray, which affects the next wall-bounce, which affects the new direction... the potential scenarios to be accounted for seem to explode.
However, the following diagram shows a possible trick:
However, the following diagram shows a possible trick:
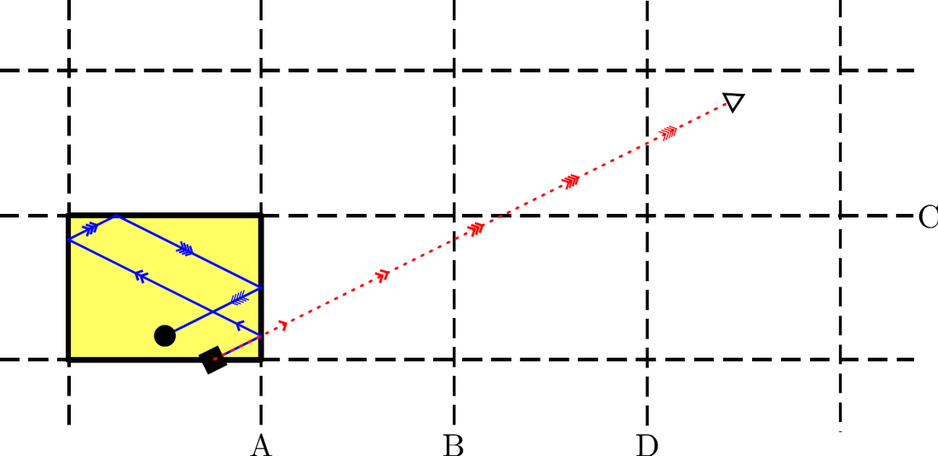
A blue light ray travels within the yellow box, bouncing off the mirrored walls. It starts from the black square and ends at the black circle. Dashed black lines mark out reflected copies of the box, while the red dotted line marks a virtual light ray which goes from the back square to the white triangle.
The red virtual light ray marks the path that the light ray would have taken if the box wasn't there. The real light ray and virtual light ray reach the single arrowhead at the same time, then the double arrowhead at the same time, and so on. But while it's hard to find the position of the blue arrowheads, the red arrowheads are rather straightforward to locate!
It remains to deduce the positions of the blue arrowheads from the red ones. The key is to realize that each bounce of the real light ray corresponds to the virtual light ray striking a virtual wall (the dashed black lines). The virtual light ray strikes lines A, B, C then D. The following process can transform the path of the virtual light ray into that of the real light ray:
How can this process be used to predict where the light ray has reached after a certain amount of time? In the first place, what variables (e.g. initial position and direction) need to be fixed and known before the prediction can happen?
It remains to deduce the positions of the blue arrowheads from the red ones. The key is to realize that each bounce of the real light ray corresponds to the virtual light ray striking a virtual wall (the dashed black lines). The virtual light ray strikes lines A, B, C then D. The following process can transform the path of the virtual light ray into that of the real light ray:
- Take the part of the path of the virtual light ray on the right of D and reflect it about D.
- Take the part of the new path above C and reflect it about C.
- Take the part of the new path to the right of B and reflect it about B.
- Take the part of the new path to the right of A and reflect it about A.
How can this process be used to predict where the light ray has reached after a certain amount of time? In the first place, what variables (e.g. initial position and direction) need to be fixed and known before the prediction can happen?
Suggestions
- What if instead of a light ray, we had a billiard ball bouncing around inside a rectangular table? (Ignore friction and whatnot.) Can the same method be used? If yes, why? If no, how can it be adapted?
- What if the light ray was bouncing in 3D, inside a cuboid box with mirrored walls?
- Stretch your imagination and consider the strangest types of boxes in any dimension or shape, and try to adapt the reflection method to them.
Note that I have seen the reflection trick inside some book before, so it is probably well-known — all the more important that investigators do a thorough literature review to see what has been tried. Chapter XI of (Berger, 2010) discusses other dimensions of this problem, but does not appear to use the trick.
References
(Berger, 2010) Mercel Berger. Geometry Revealed: A Jacob's Ladder to Modern Higher Geometry. Springer-Verlag Berlin Heidelberg (2010).
Determinants in Terms of Matrix Multiplication
This came from a previous post. The determinant of a $2 \times 2$ matrix $\mathbf{A}$ has a simple formula:\begin{equation}
\det\mathbf{A} = \det\begin{bmatrix}
a & b\\
c & d
\end{bmatrix}
= ad - bc
\end{equation}It can be verified that we could also express it as
\begin{equation}
\det\mathbf{A} =
\begin{bmatrix}
1 & 0
\end{bmatrix}\mathbf{A}^\mathsf{T}
\begin{bmatrix}
0 & 1\\
-1 & 0
\end{bmatrix}\mathbf{A}
\begin{bmatrix}
1\\0
\end{bmatrix}.
\end{equation}
\det\mathbf{A} = \det\begin{bmatrix}
a & b\\
c & d
\end{bmatrix}
= ad - bc
\end{equation}It can be verified that we could also express it as
\begin{equation}
\det\mathbf{A} =
\begin{bmatrix}
1 & 0
\end{bmatrix}\mathbf{A}^\mathsf{T}
\begin{bmatrix}
0 & 1\\
-1 & 0
\end{bmatrix}\mathbf{A}
\begin{bmatrix}
1\\0
\end{bmatrix}.
\end{equation}
Suggestions
- Verify the formula.
- Formulate a general version of this kind of formula for a determinant of an $n \times n$ matrix. Laplace expansion would probably be useful.
- Prove the generalized formula. Mathematical induction would probably be useful.
Game of Life and other Cellular Automata
Conway's Game of Life is a mathematical simulation that produces "lifelike" results from very simple input and simulation rules. In an infinite 2D grid of squares, some are "alive" while the others are "dead". Some rules are used to calculate from the current distribution of live and dead squares a new distribution, or "pattern", of live and dead squares, and the same rules are used to take this new pattern and calculate the next pattern, and so on. The Wikipedia article on this "game" provides a good introduction, featuring:
- Patterns that never change (still lifes)
- Patterns that change but repeat themselves after a number of steps (oscillators)
- Patterns that rapidly explode into chaos
- Patterns that "travel" in a certain direction (spaceships)
- Patterns that repeat themselves but shoot out spaceships at regular intervals (see the illustration below)
- Patterns that can replicate themselves somewhere else on the grid
- Patterns that, when you look from far away, simulate the Game of Life itself (metacells)
What other interesting patterns can you come up with? Can you change the rules or setup of the game, yet still define some new, interesting patterns?
Suggestions
- How about a higher-dimensional grid?
- How about a triangular or hexagonal grid?
- How about letting each cell have more than two states?
This proposal is probably the most open-ended one, but this game is very famous so it's extremely important to find out what interesting structures have been defined by other researchers already.

The content of Mathematics Research Proposals by Cheng Herng Yi, except the figures whose captions are prefixed by (*), is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.