Modular Polyhedra from Waterbomb Base Units
Brainstorming for an origami math workshop for Grade 8 students, I tried to think of origami models that were:
- Easy to fold,
- Had "mathematical elegance", and
- Could be an entry point to math discussions.
|
|
If you can't view the applet on an updated browser, check for compatibility. Mobile users on Android are advised to view this page using Firefox.
|
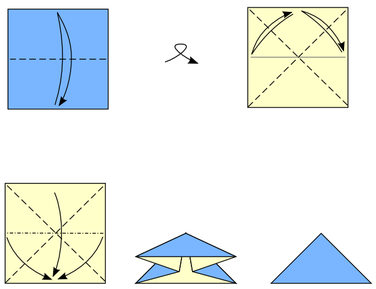
Each waterbomb base is very easy to fold:
|
6 waterbomb base units are needed to assemble an octahedron.
|
During the actual workshop, many of the students were smart enough to figure the assembly out, so you should also try to figure it out from these photographs. It's easier if each waterbomb base has a unique color. If you're lazy to figure out, more clues are at the bottom of this post.
Other Solids?
While designing the workshop I thought that maybe the waterbomb base units could be assembled into other geometric solids. I tried to make a cuboctahedron and failed, unexpectedly producing a square antiprism:
|
|
|
Important: smaller modules are easier to assemble into solids that are stable (don't fall apart) and portable.
I asked the students the following questions about any solid that can be assembled from the units:
The answers led to a set of criteria for us to choose new solids that could be assembled. Among the Platonic solids the following passed the test:
I asked the students the following questions about any solid that can be assembled from the units:
- Q: What kinds of faces can it have? A: Square or triangle faces.
- Q: How many faces can there be around each corner? A: At most four.
- Q: How many units are needed to assemble it? A: One unit is needed per corner.
The answers led to a set of criteria for us to choose new solids that could be assembled. Among the Platonic solids the following passed the test:
The octahedron is familiar, but how can the cube be assembled if only 3 faces meet at each corner (a "degree 3 vertex") but each unit has 4 "flaps"? The solution is to eliminate one flap by assembling the following subunit:
This subunit accommodates degree 3 vertices.
4 of them can be assembled into a cube as follows:
|
|
|
(But each subunit eliminates one flap from each waterbomb base to give two degree 3 vertices - what if we have an odd number of degree 3 vertices? Readers familiar with graph theory will note that the "Handshake Lemma" guarantees that won't happen.)
Sadly the tetrahedron can't be assembled in this way because the paper will clash internally. More possible solids follow; the weird-looking ones are Johnson solids, which are pretty different from the usual "ball-shaped" Platonic solids or Archimedean solids.
Sadly the tetrahedron can't be assembled in this way because the paper will clash internally. More possible solids follow; the weird-looking ones are Johnson solids, which are pretty different from the usual "ball-shaped" Platonic solids or Archimedean solids.
Triangular Prism
Assembling 3 of the subunits together in the same way yields a triangular prism.
|
|
|
|
Gyrobifastigium
"Joining" two triangular prisms together yields a gyrobifastigium.
|
|
|
|
Augmented Triangular Prism
Or you could "stick" a pyramid onto a triangular prism to form an augmented triangular prism.
|
|
|
|
Square Pyramid
A square pyramid by itself can be obtained by pulling one unit out of the octahedron and tucking the exposed flaps into each other nicely.
|
|
|
|
Elongated Square Pyramid
"Stacking" a square pyramid onto a cube yields an elongated square pyramid, which looks like a house.
|
|
|
|
Challenge
Can you assemble these? (You might need a bit of glue...) What others can you make?
Assembling the Octahedron
The only clue I'll give on how to assemble the units is the following picture for the octahedron:
