Origami Research and Applications
The uses of origami are not confined to artistic expression. Insights from folding paper have been applied to space technology, automobiles, medicine and programmable matter; these applications began to appear a few decades ago. At heart is the mathematics behind the humble piece of paper, which was studied as early as the 1930s. The mathematics gives rise to challenging unsolved problems and software that design complex origami on-demand.
This article lists some of the more accessible research as it is meant as a primer to origami research, but it may be somewhat outdated.
This article lists some of the more accessible research as it is meant as a primer to origami research, but it may be somewhat outdated.
Origami in Technology
Several technological products have been based on origami. These devices are flat and sheet-like, and they need to change their shape often, so that they can be stored and transported compactly but expand to full size for usage. The reversible folding motions of a sheet make origami the perfect answer. USA’s National Science Foundation has recognized this potential, giving USD14M of awards to projects related to “Origami Design for Integration of Self-assembling Systems for Engineering Innovation (ODISSEI).”
Solar Panels for a Satellite (1995)
|
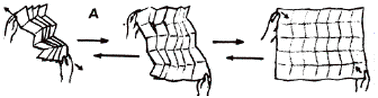
In 1955, Japanese scientists used an origami technique, the Miura map fold, to fold the huge solar panels of a satellite into a small package. After the satellite entered space, the solar panels unfolded to full size and functionality.
Opening the Miura map fold
Image source: http://www.kobe-du.ac.jp/gsdr/gsdr/kiso04/01-e.html
|
Artist's impression of a satellite with the Miura map fold
|
Airbag Simulations
To ensure that the airbag of a car will inflate properly when it crashes, copies of the car will often need to be crashed in real life. However, modeling the folding surface of the airbag using origami allows engineers to replace real crash tests with computer simulations.
|
|
|
Image source: Robert J. Lang. The math and magic of origami. TED.com (2008).
Origami Stent Graft (2003)
Closed and open forms of the stent graft
Researchers from the University of Oxford developed an origami stent graft, a tube-shaped medical device used to hold arteries open during surgery. The metal tube would be folded into a thinner shape using a special origami pattern. It would then be inserted into an artery, where body heat would cause it to unfold and expand, holding the artery open.
Image source: http://www-civil.eng.ox.ac.uk/people/zy/old/research/stent.pdf
Image source: http://www-civil.eng.ox.ac.uk/people/zy/old/research/stent.pdf
Other Technologies
Structural Origami
Deployable Structures: Structures that have different initial and final configurations, folding from one to the other
Deployable Structures: Structures that have different initial and final configurations, folding from one to the other
- Industrial packaging
- Self-folding microscopic origami driven by cellular traction or surface tension
- Programmable matter (structures that automatically fold to desired shapes on command)
Automated Origami Design
Programmers have written software that allow users to specify a desired origami shape and calculate its blueprint (crease pattern) based on that data. Varying programs have been written to design different types of origami, from animals to geometric shapes.
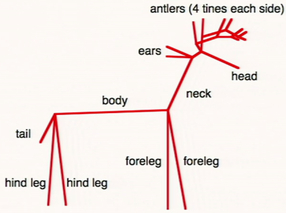
Treemaker (1998)
Robert J. Lang developed the mathematics needed to generate a pattern of lines that folds into a specified stick figure, automating the design of animal origami.
Stick figure representing the subject
|
Crease pattern ("folding instructions")
|
Final folded product
|
Image source: Robert J. Lang. The math and magic of origami. TED.com (2008).
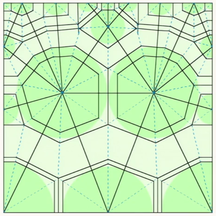
Origamizer (2008)
Tomohiro Tachi wrote this computer program to generate a blueprint that folds into a desired 3D shape with flat sides.
User-specified 3D shape, and the computed crease pattern
|
Final folded product
|
Image source: Tomohiro Tachi. Origamizing polyhedral surfaces. IEEE Transactions on Visualization and Computer Graphics 16, 298-311 (2010).
Other Automated Origami Design Algorithms
- Axial symmetric polyhedra by myself
- "Maze Folder" by Erik D. Demaine, Martin L. Demaine and Jason Ku that designs orthogonal mazes.
- Polycubes (3D solids composed of cubes glued together at their faces) by Aviv Ovadya
- "ORI-REF" by Jun Mitani that designs curved origami
- "ORI-REVO" by Jun Mitani that folds rotationally symmetric polyhedra
Origami Mathematics
Creases on paper form lines. Different creases meet in point and form angles. Naturally, origami is deeply tied to geometry. Seeing an origami model as a mathematical object obeying certain mathematical “laws of folding” is at the heart of every computer program used in Automated Origami Design. Problems in mathematics itself have even been solved using origami techniques.
Flat-foldable Origami
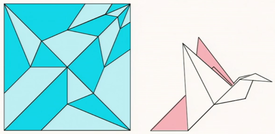Crease pattern of a flat-folded bird
Much of origami is folded into a flat product before it is shaped into a more lifelike 3D form. Observations regarding the blueprints of flat origami formed the early “laws of folding”. One such “law” is that the regions that the blueprint divides the paper into can be colored in two colors so that no neighboring regions have the same color.
Image source: Robert J. Lang. The math and magic of origami. TED.com (2008).
Image source: Robert J. Lang. The math and magic of origami. TED.com (2008).
Fold-and-Cut Problem
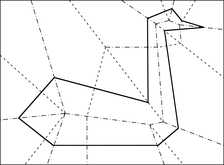Fold-and-cut swan
A magic trick involved cutting out paper shapes such as stars by folding a piece of paper and making one straight cut. The mathematical problem of what shapes could be produced in this manner was solved by Demaine et al, who showed that any shape with straight sides was possible.
Image source: http://erikdemaine.org/foldcut/
Image source: http://erikdemaine.org/foldcut/
Other Mathematics in Origami
Beyond geometry, origami also has connections to matrices & linear algebra, abstract algebra, combinatorics, topology, differential equations and many other fields. Computational origami, the study of origami algorithms, is also an active area of research.
OSME Conferences
Worldwide origami research
Many of the above pieces of research were presented at the International Conference on Origami in Science, Mathematics and Education (OSME), which inspired researchers and provided a platform for them to discuss and learn of the newest developments.
In 1989, origami researchers gathered in Ferrara, Italy for the First International Meeting of Origami Science and Technology (1OSME), where they discussed their research findings and explored new directions. This has since evolved into a highly successful series of OSME conferences. They link separate research groups from around the world, forming an international community for origami research.
Educational uses of origami have been a focus since 3OSME, the third conference in 2001. This acknowledges the possibilities of origami in demonstrating abstract geometric concepts through fun and engaging hands-on activities.
In 1989, origami researchers gathered in Ferrara, Italy for the First International Meeting of Origami Science and Technology (1OSME), where they discussed their research findings and explored new directions. This has since evolved into a highly successful series of OSME conferences. They link separate research groups from around the world, forming an international community for origami research.
Educational uses of origami have been a focus since 3OSME, the third conference in 2001. This acknowledges the possibilities of origami in demonstrating abstract geometric concepts through fun and engaging hands-on activities.
Further Resources
Many more examples of origami research and applications can be found in:
Some videos are excellent introductions to origami:
Some books go into more detail about origami mathematics and computer science:
- OSME conference proceedings: 3OSME, 4OSME, 5OSME
- The conference programs have links to the abstracts: 4OSME, 5OSME
Some videos are excellent introductions to origami:
- Between the Folds: an award-winning documentary on origami and its relations to art, science and education.
- Robert J. Lang's TEDTalk "The math and magic of origami".
Some books go into more detail about origami mathematics and computer science:
- Origami Design Secrets by Robert J. Lang
- Project Origami by Thomas C. Hull
- Geometric Folding Algorithms: Linkages, Origami Polyhedra by Erik D. Demaine and Joseph O'Rourke
The content of Origami Research and Applications by Cheng Herng Yi, except for the attributed figures, is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.