This is an exploration of some interesting parallels.

One might say that the categories of geometry and algebra cover most of mathematics. I think most mathematicians see them not as categories but as different ways to see the same object. Time and again, geometric intuition uncovers hidden dimensions in algebraic objects: the algebraic geometric of elliptic curves, as well as the standard practice of studying a large set of functions by considering each function as a point in a "function space," serve as ready examples. On the other hand, geometric spaces that we're interested in, such as the fabric of space-time, or crystal lattices, often have underlying symmetries that can be encoded as algebraic structures which afford us a compact, high-level language to state and prove far-reaching claims on the properties of the geometry.

Why are these two viewpoints so effective, so illuminating, so incisive? If we see geometric intuition as an extension of our human capability for spatial visualization and reasoning, then I'd say that's a pretty fundamental source for geometric intuition—an internalization of our everyday visual and tactile interaction with out environment. What about algebra then? We could tie it to our faculties of language, which associate meanings to symbols or strings of them (literally called a word in group theory), communicate that meaning, and process the information in the symbols by manipulating them. We really do have a "language of algebra." So the first parallel goes from geometry and algebra to spatial reasoning and linguistic ability.

But I like to go even further, rise higher in abstraction: is there any more fundamental difference, or similarity, between our faculties of spatial reasoning and language? How about space vs. time? Obviously geometry is space. If we think of multiplication in algebra as composing transformations one after the other, such as the linear transformations in linear algebra (Cayley's theorem guarantees that we can view any group as a transformation group), then algebra is a form of "discrete time travel."

What about other fields of math? If geometry is space and algebra is time, then perhaps analysis is change, and topology is connection.

(This post is for prospective freshmen enrolling in the Massachusetts Institute Technology. I wish I knew all this early enough, so now I'm telling it to you!)

Origami? Folding bits of paper? You mean that children's pastime? It can't possibly be of any "real" use, right?
What if I told you that origami has been applied in space technology?

The 6th International Meeting on Origami in Science, Mathematics and Education (6OSME) was held in Tokyo University in August to help origami researchers, artists and educators share their ideas on the connections between origami and a wide range of other fields, including applications in theory and industry.

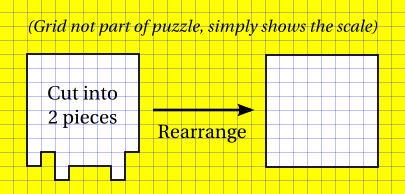
One of the talks I usually give is on geometric dissections, which I begin with the following puzzle from (Lindgren 1964):

I thought it might have been more fun to give the puzzle to the prospective audience one week before I actually presented the solution, so I did that for an upcoming presentation on geometric dissections for students from Raffles Girls' School. I hope they got very frustrated by the puzzle. I also promised to give a hint to the puzzle, but I forgot to post it! Highlight the hint if you want to read it...

Lindgren, Harry (1964). Geometric Dissections.  D. Van Nostrand.

There was this thing going on Facebook:

I was given Stefan Banach (Poland). I will not discuss the Banach-Tarski Paradox.

Stefan Banach was one of the 20th century's greatest mathematicians. His self-taught prowess impressed the renowned Prof. Hugo Steinhaus, who supported Banach's career. His doctoral thesis sparked and grew into the field of "Functional Analysis", which has proved fundamental to Quantum Mechanics and Differential Equations (used widely in engineering). During World War II he and fellow academics were sheltered from Nazi persecution by employment as "lice feeders" at a Typhus Research Institute. (from Wikipedia)

He proved that:

1. Throw a world map on the floor. There's always a way to hammer a nail through the map and the floor so that the nail's position on the map exactly corresponds to its actual location.
2. Take a piece of paper, fold a paper airplane and press it flat within the original boundary of the paper. One of the points in the paper has been returned to its original position.

These are consequences of the Banach fixed-point theorem, which actually says that if we "shrink" the world (e.g. into a "map") so every pair of points can only get closer (this also happens when folding), there will be a "fixed point". The world might be (1) Earth, (2) a piece of paper or some other strange, convoluted, theoretical world.

This is one of many "fixed-point theorems", all of which say that if you take a "world", transform it so-and-so, then some point in the world must have remained immobile. The more famous Brouwer fixed-point theorem has been applied in Economics, to show that markets (the "world") have "fixed points" (e.g. balances between supply and demand).

I must thank a friend for telling me a basic form of this layman explanation many years ago; it has stuck with me all these years.

If you're studying undergrad math, physics or chemistry, chances are you've heard of this thing called a "Group" that is studied in "Group Theory". What is it and why is it so important? I'll explain in a simple way.

The most familiar group is our number system; we have a bunch of numbers, and we have this thing called "$+$" which can take two numbers and churn out another number. A group is just a set of objects, and you have one "operation" (usually called "$\ast$" or "$+$", but those are just names) that tells you how to combine objects to produce other objects in that set, subject to a few rules. Why devise such a "strange chasing game" in a set of objects? That's because such systems are omnipresent in a stupendous array of phenomena:

In the previous article we saw that fruitful analogies between finitary and infinitary mathematics can allow the techniques of one to shed light on the other. Here we borrow the power of infinitary math—in particular, ultrafilters and non-standard analysis—to simplify proofs of finitary statements.

Part 5 of a six-part series of adaptations from Terence Tao’s book “Structure and Randomness".

Readers need some familiarity with sentences like "for every $\varepsilon$ there exists a large $N$ such that..." or its symbolic equivalent, "$\forall\varepsilon: \exists N: \dotsc$".

A rough idea of big O notation would also be helpful but is not necessary. A brief introduction: we say that $f(x) = O(g(x))$ (as $x \to \infty$) to mean that the "growth" of $f(x)$ is "bounded above" by $g(x)$; more formally, there exist positive real numbers $M$ and $x_0$ such that $\lvert f(x)\rvert \leq M\lvert g(x)\rvert$ for all $x > x_0$.

Note that $\lvert x\rvert$ denotes the absolute value of $x$, not its cardinality as indicated in Part 4.

Analysis (something like an advanced calculus) is often differentiated into "hard analysis" ("quantitative", "finitary") and "soft analysis" ("qualitative", "infinitary"). Discrete math, computer science, and analytic  number theory normally uses hard analysis while operator algebra, abstract harmonic analysis, and ergodic theory tend to rely on soft analysis. The field of partial differential equations uses techniques from both.

Convenient notation (e.g. $O(\:)$) from qualitative analysis can conceal gritty details from quantitative and argue efficiently from the big picture, at the cost of a precise description. Conversely, quantitative analysis can be seen as a more precise and detailed refinement of qualitative analysis. The intuitions, methods and results in hard analysis often have analogues in soft analysis and vice versa, despite their contrasting language. Tao argues this technique transfer can benefit both disciplines. Table 5 features a rough "dictionary" between the notational languages of soft and hard analysis. Kudos to Tao for such an illuminating comparison!

Table 5: "Translating" soft analysis to hard analysis [1.3]

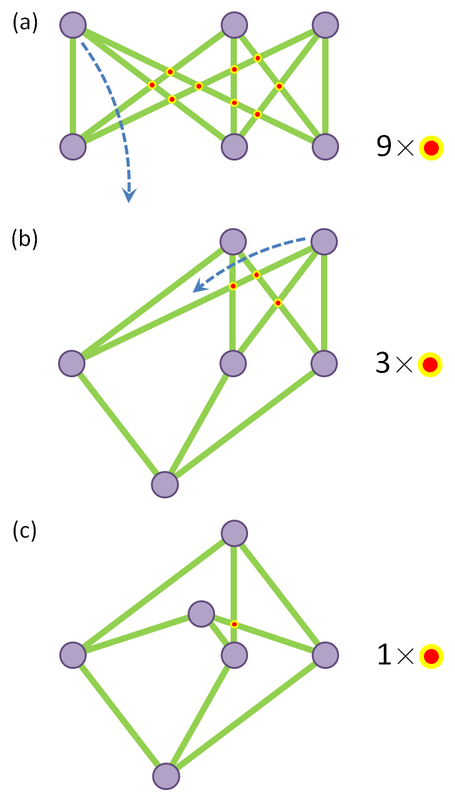
A graph $G = (V, E)$ is a set $V$ of vertices ("objects") and a set $E$ of edges ("relationships between two objects"). For example, $V$ could be a set of people and $E$ the set of friendships (Facebook really uses this social graph to analyze user behavior). $V$ could also be the set of airports and $E$ the set of flights from one airport to another. The immense flexibility of this definition allow graphs to model and analyze a tremendous variety of real-life situations, but here we are interested in the abstract representation of a graph, in particular its drawing. The focus is on applying the technique of amplification, which was presented in Part 3 of this series.

A drawing of graph $G = (V, E)$ simply draws the vertices in $V$ as dots on the plane, and the edges $E$ as lines (or curves) connecting them. $G$ can have many possible drawings, in which the edges can have different numbers of crossings between pairs of edges (i.e. three concurrent edges have 3 crossings). Fig. 4(a)-(c) features three drawings of the $K_{3, 3}$ graph with different numbers of crossings.

Given an inequality $f(x) \leq g(x)$ with imbalances in symmetry between the left-hand side (LHS) and right-hand side (RHS), amplification is a mathematical trick that can exploit that imbalance to derive a stronger inequality (i.e. the LHS and RHS are closer). As for why mathematicians might need such a technique, see "Why do we need strong inequalities?" below.

Consider some transformations $T$ that change $x$ such that $g$, but not $f$, is "symmetric" relative to $T$. That is, $f(T(x)) \leq g(T(x)) = g(x)$. Then we can choose $T$ to maximize the LHS $f(T(x))$ and "tighten" the inequality. Let's illustrate this trick by applying it to prove the Cauchy-Schwarz Inequality (actually, the special case of the familiar $n$-dimensional space $\mathbb{R}^n$):
$$\lvert\mathbf{v} \cdot \mathbf{w}\rvert \leq \lVert\mathbf{v}\rVert\lVert\mathbf{w}\rVert \text{ for all } \mathbf{v}, \mathbf{w} \in \mathbb{R}^n \tag{3.1}$$