|
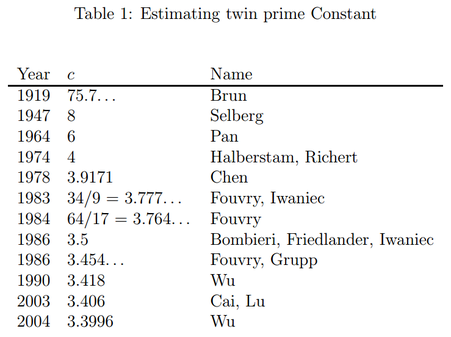
Part 3 of a six-part series of summaries and adaptations from Terence Tao's book "Structure and Randomness". [1.9] Amplification, arbitrage, and the tensor power trickGiven an inequality $f(x) \leq g(x)$ with imbalances in symmetry between the left-hand side (LHS) and right-hand side (RHS), amplification is a mathematical trick that can exploit that imbalance to derive a stronger inequality (i.e. the LHS and RHS are closer). As for why mathematicians might need such a technique, see "Why do we need strong inequalities?" below. Consider some transformations $T$ that change $x$ such that $g$, but not $f$, is "symmetric" relative to $T$. That is, $f(T(x)) \leq g(T(x)) = g(x)$. Then we can choose $T$ to maximize the LHS $f(T(x))$ and "tighten" the inequality. Let's illustrate this trick by applying it to prove the Cauchy-Schwarz Inequality (actually, the special case of the familiar $n$-dimensional space $\mathbb{R}^n$): $$\lvert\mathbf{v} \cdot \mathbf{w}\rvert \leq \lVert\mathbf{v}\rVert\lVert\mathbf{w}\rVert \text{ for all } \mathbf{v}, \mathbf{w} \in \mathbb{R}^n \tag{3.1}$$ Discard the trivial case of either $\mathbf{v}$ and $\mathbf{w}$ being a zero vector. The dot product $\mathbf{v} \cdot \mathbf{w}$ and norms (self-dot product) like $\lVert\mathbf{v}\rVert$ suggest expanding the (nonnegative) dot product $(\mathbf{v} - \mathbf{w}) \cdot (\mathbf{v} - \mathbf{w})$ into $$\lVert\mathbf{v}\rVert^2 - 2(\mathbf{v} \cdot \mathbf{w}) + \lVert\mathbf{w}\rVert^2 \geq 0 \implies \mathbf{v} \cdot \mathbf{w} \leq \dfrac12\lVert\mathbf{v}\rVert^2 + \dfrac12\lVert\mathbf{w}\rVert^2.$$ The vector norm (and by extension, the RHS) is symmetric relative to dilation by factor $(-1)$ (i.e. flip each point 180° about the origin) but the LHS is not. So we choose the transformation $T(\mathbf{v}) = -\mathbf{v}$. This gives $$\pm\mathbf{v} \cdot \mathbf{w}\leq \dfrac12\lVert\mathbf{v}\rVert^2 + \dfrac12\lVert\mathbf{w}\rVert^2 \implies \lvert\mathbf{v} \cdot \mathbf{w}\rvert \leq \dfrac12\lVert\mathbf{v}\rVert^2 + \dfrac12\lVert\mathbf{w}\rVert^2.$$ The inequality has been tightened by increasing the LHS, but the RHS is still too big. This is because $\frac12\lVert\mathbf{v}\rVert^2 + \frac12\lVert\mathbf{w}\rVert^2 \geq \lVert\mathbf{v}\rVert\lvert\mathbf{w}\rVert$ (easily derived by expanding $(\lVert\mathbf{v}\rVert - \lVert\mathbf{w}\rVert)^2 \geq 0$). We reduce the RHS by exploiting another imbalance in symmetry, this time of a "homogenisation" transformation $T_\lambda(\mathbf{v}, \mathbf{w}) = (\lambda\mathbf{v}, \mathbf{w}/\lambda)$ which scales the first vector by $\lambda$ and the second by $1/\lambda$, which keeps the product of their lengths the same. Thus the dot product (and by extension, the LHS) is symmetric relative to $T_\lambda$ but the RHS is not, which gives $$\lvert\mathbf{v} \cdot \mathbf{w}\rvert = \lvert(\lambda\mathbf{v}) \cdot (\mathbf{w}/\lambda)\rvert \leq \dfrac{\lambda^2}2\lVert\mathbf{v}\rVert^2 + \dfrac1{2\lambda^2}\lVert\mathbf{w}\rVert^2.$$ Finally we minimize the RHS by setting $\lambda = \lVert\mathbf{w}\rVert/\lVert\mathbf{v}\rVert$ to get Eq. (3.1). We have "amplified" our way into the Cauchy-Schwarz Inequality! $$\lvert\mathbf{v} \cdot \mathbf{w}\rvert \leq \lVert\mathbf{v}\rVert\lVert\mathbf{w}\rVert \text{ for all } \mathbf{v}, \mathbf{w} \in \mathbb{R}^n \tag{3.1}$$ Further discussionFor another insight to Eq. (3.1), consider that $\mathbf{u} \cdot \mathbf{v} = \lVert\mathbf{v}\rVert\lVert\mathbf{w}\rVert\cos\theta$. The "magical cheating" of amplification can produce amazingly strong inequalities, that are difficult to prove otherwise, from comparatively weak or even trivial inequalities. However, from another perspective, this means that the strong and weak inequalities were equivalent in the first place! Our vision was simply obstructed and misled by low-quality versions of the strong inequality. Tao's original blog post [1.9] exploits more symmetry imbalances - via dilation, homogenity, linearity and phase rotation (for complex numbers) to amplify an astonishing variety of inequalities in harmonic analysis. Even symmetry via Cartesian Products can be exploited to amplify the following inequality on cardinalities of sumsets (do check the definition), $$\lvert kB\rvert \leq \dfrac{\lvert A + B\rvert^k}{\lvert A\rvert^{k - 1}}$$ into the more general inequality $$\lvert B_1 + \dotsb + B_k\rvert \leq \dfrac{\lvert A + B_1\rvert \dotsm \lvert A + B_k\rvert }{\lvert A\rvert^{k - 1}}.$$ This intrigued me for two reasons - this was a rather "discrete" inequality (mostly involving integers) as opposed to the "continuous" nature of the Cauchy-Schwarz Inequality, and amplification was used to generalize, not merely to strengthen inequalities! For the sake of readers unfamiliar with inequalities, I feel that I need to explain beyond what Tao did: Why do we need strong inequalities?Many properties and quantities in math are difficult or impossible to calculate exactly (e.g. the number of twin primes below some $N$ (primes differing by $2$, like $11$ and $13$) or the position or momentum of particles), so we often establish upper or lower bounds on them to at least give some idea of the size of the quantity. Conjecturing is now somewhat easier with computer methods (e.g. plot a graph of "number of twin primes $f(x)$ below $x$" versus $x$ and look at the graph shape) but how do we prove a bound $f(x) \leq g(x)$? We could start off with known inequalities and add them together, multiply or somehow manipulate them into some $f_0(x) \leq g_1(x)$, where hopefully (A) $f(x) \leq f_0(x)$ and (B) $g_1(x) \leq g(x)$. Naive attempts usually fail because we either violate (A) or (B). Such failure gets more likely if the gap between $f(x)$ and $g(x)$ is narrow; such an inequality $f(x) \leq g(x)$ is called "tight", "strong" or "powerful". Failure increases because an inequality that is "too weak" (LHS and RHS are too far apart) may participate in our manipulations, bloating the gap between $f_0(x)$ and $g_1(x)$ and preventing us from "squeezing" both of them between $f(x)$ and $g(x)$. So we need to be extra careful to use only strong inequalities in our manipulations, which requires many strong inequalities to be available in the first place. Strong inequalities are so useful that they can give rise to quick proofs of difficult inequalities. Of course, after we prove our conjecture $f(x) \leq g(x)$, ambitious souls might attempt to tighten the bound further. "Is this the most we can estimate about $f(x)$? Could we improve our knowledge of its size?" Strengthening techniques such as amplification might then lend a hand. For instance, an upper bound of the aforementioned number of twin primes $f(x)$ below $x$ is known to be $$f(x) < c\left(\dfrac{Cx}{(\ln x)^2}\right) \text{ where } C = 2\prod\limits_{\text{prime } p > 2}\left(1 - \dfrac{1}{(p - 1)^2}\right) \approx 1.32032$$. The smaller the constant $c$, the tighter the upper bound, but the harder is is to prove that the inequality still holds. The history of improvement on the value of the twin prime constant $c$ (as proven to be possible) by various researchers is summarized in the following table (Nazardonyavi, 2012): Interested readers can check out the proof of the best known bound (Wu, 2004). References
0 Comments
Leave a Reply. |
Archives
December 2020
Categories
All
|
 RSS Feed
RSS Feed