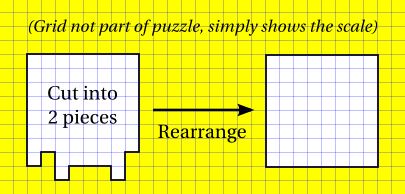
One of the talks I usually give is on geometric dissections, which I begin with the following puzzle from (Lindgren 1964):

I thought it might have been more fun to give the puzzle to the prospective audience one week before I actually presented the solution, so I did that for an upcoming presentation on geometric dissections for students from Raffles Girls' School. I hope they got very frustrated by the puzzle. I also promised to give a hint to the puzzle, but I forgot to post it! Highlight the hint if you want to read it...

Lindgren, Harry (1964). Geometric Dissections.  D. Van Nostrand.

There was this thing going on Facebook:

I was given Stefan Banach (Poland). I will not discuss the Banach-Tarski Paradox.

Stefan Banach was one of the 20th century's greatest mathematicians. His self-taught prowess impressed the renowned Prof. Hugo Steinhaus, who supported Banach's career. His doctoral thesis sparked and grew into the field of "Functional Analysis", which has proved fundamental to Quantum Mechanics and Differential Equations (used widely in engineering). During World War II he and fellow academics were sheltered from Nazi persecution by employment as "lice feeders" at a Typhus Research Institute. (from Wikipedia)

He proved that:

1. Throw a world map on the floor. There's always a way to hammer a nail through the map and the floor so that the nail's position on the map exactly corresponds to its actual location.
2. Take a piece of paper, fold a paper airplane and press it flat within the original boundary of the paper. One of the points in the paper has been returned to its original position.

These are consequences of the Banach fixed-point theorem, which actually says that if we "shrink" the world (e.g. into a "map") so every pair of points can only get closer (this also happens when folding), there will be a "fixed point". The world might be (1) Earth, (2) a piece of paper or some other strange, convoluted, theoretical world.

This is one of many "fixed-point theorems", all of which say that if you take a "world", transform it so-and-so, then some point in the world must have remained immobile. The more famous Brouwer fixed-point theorem has been applied in Economics, to show that markets (the "world") have "fixed points" (e.g. balances between supply and demand).

I must thank a friend for telling me a basic form of this layman explanation many years ago; it has stuck with me all these years.