Part 5 of a six-part series of adaptations from Terence Tao’s book “Structure and Randomness".

Readers need some familiarity with sentences like "for every $\varepsilon$ there exists a large $N$ such that..." or its symbolic equivalent, "$\forall\varepsilon: \exists N: \dotsc$".

A rough idea of big O notation would also be helpful but is not necessary. A brief introduction: we say that $f(x) = O(g(x))$ (as $x \to \infty$) to mean that the "growth" of $f(x)$ is "bounded above" by $g(x)$; more formally, there exist positive real numbers $M$ and $x_0$ such that $\lvert f(x)\rvert \leq M\lvert g(x)\rvert$ for all $x > x_0$.

Note that $\lvert x\rvert$ denotes the absolute value of $x$, not its cardinality as indicated in Part 4.

Analysis (something like an advanced calculus) is often differentiated into "hard analysis" ("quantitative", "finitary") and "soft analysis" ("qualitative", "infinitary"). Discrete math, computer science, and analytic  number theory normally uses hard analysis while operator algebra, abstract harmonic analysis, and ergodic theory tend to rely on soft analysis. The field of partial differential equations uses techniques from both.

Convenient notation (e.g. $O(\:)$) from qualitative analysis can conceal gritty details from quantitative and argue efficiently from the big picture, at the cost of a precise description. Conversely, quantitative analysis can be seen as a more precise and detailed refinement of qualitative analysis. The intuitions, methods and results in hard analysis often have analogues in soft analysis and vice versa, despite their contrasting language. Tao argues this technique transfer can benefit both disciplines. Table 5 features a rough "dictionary" between the notational languages of soft and hard analysis. Kudos to Tao for such an illuminating comparison!

Table 5: "Translating" soft analysis to hard analysis [1.3]

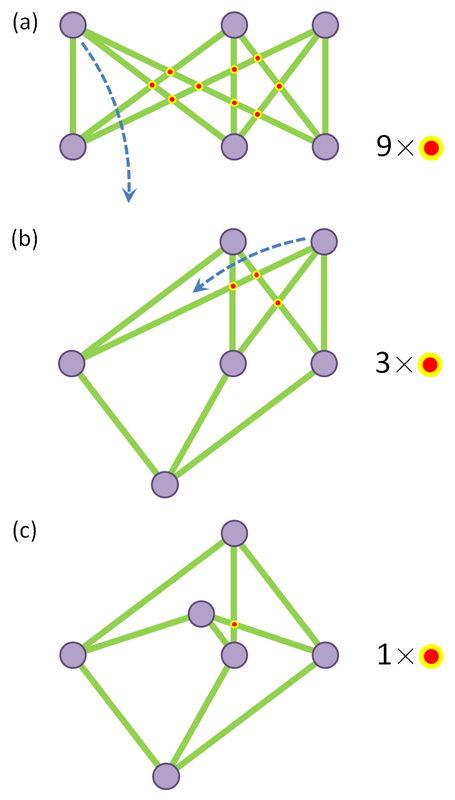
A graph $G = (V, E)$ is a set $V$ of vertices ("objects") and a set $E$ of edges ("relationships between two objects"). For example, $V$ could be a set of people and $E$ the set of friendships (Facebook really uses this social graph to analyze user behavior). $V$ could also be the set of airports and $E$ the set of flights from one airport to another. The immense flexibility of this definition allow graphs to model and analyze a tremendous variety of real-life situations, but here we are interested in the abstract representation of a graph, in particular its drawing. The focus is on applying the technique of amplification, which was presented in Part 3 of this series.

A drawing of graph $G = (V, E)$ simply draws the vertices in $V$ as dots on the plane, and the edges $E$ as lines (or curves) connecting them. $G$ can have many possible drawings, in which the edges can have different numbers of crossings between pairs of edges (i.e. three concurrent edges have 3 crossings). Fig. 4(a)-(c) features three drawings of the $K_{3, 3}$ graph with different numbers of crossings.

Given an inequality $f(x) \leq g(x)$ with imbalances in symmetry between the left-hand side (LHS) and right-hand side (RHS), amplification is a mathematical trick that can exploit that imbalance to derive a stronger inequality (i.e. the LHS and RHS are closer). As for why mathematicians might need such a technique, see "Why do we need strong inequalities?" below.

Consider some transformations $T$ that change $x$ such that $g$, but not $f$, is "symmetric" relative to $T$. That is, $f(T(x)) \leq g(T(x)) = g(x)$. Then we can choose $T$ to maximize the LHS $f(T(x))$ and "tighten" the inequality. Let's illustrate this trick by applying it to prove the Cauchy-Schwarz Inequality (actually, the special case of the familiar $n$-dimensional space $\mathbb{R}^n$):
$$\lvert\mathbf{v} \cdot \mathbf{w}\rvert \leq \lVert\mathbf{v}\rVert\lVert\mathbf{w}\rVert \text{ for all } \mathbf{v}, \mathbf{w} \in \mathbb{R}^n \tag{3.1}$$

This'll be quick; the only part of the original blog post that I understood comfortably was the brief (and slightly inaccurate) explanation of traditional image compression. It's how image formats like JPEG can reduce the memory space needed by an image file drastically while losing only a bit of quality.

Tao uses the analogy of the game Tomb Raider as a model to give some intuition for the reasons behind the "weird" consequences of quantum mechanics (QM), in particular the so-called "many worlds interpretation". The game consists of two worlds:

• Internal System: Lara Croft, the protagonist, needs to navigate tombs and solve the puzzles in them to survive. Suppose that she is intelligent and independent of the Player of the game.
• External System: the Player of the game can view the game world and "save" the game to "restore" it when Lara dies. "Restoring" resets Lara's memory (well, she simply went back to an "earlier state", right?). Unfortunately, he cannot see inside the tombs, which limits his assistance.

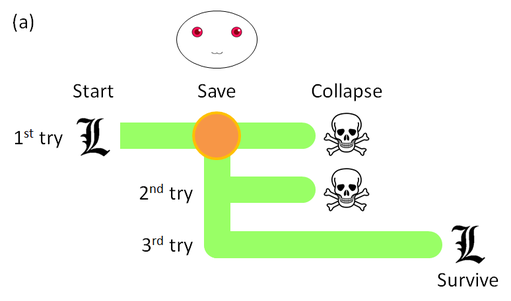
(At this point, Tao apologizes for the violent analogy. Well, I've added a little drama... and fixed a loophole.)

Each save point before a lethal puzzle causes Lara's world (from her point of view) to split into many possible "developments",  some of which involve her failure to solve the puzzle and thus death, while others have her survive. Figure 1 illustrates a sample puzzle: A tomb whose only exit a wooden trapdoor on the floor that leads to an underground passage. The tomb will collapse in, say, five minutes, and Lara ("L") must escape through the passageway, but the trapdoor is locked. The Player (smiley face) helps by creating a save point.