Next week I'm conducting an origami math workshop for Grade 8 students, and one of the activities will be to fold a skeletal octahedron (really simple modular origami). The students will be asked to choose between five octahedra I already folded in various colors, to see what kind of color schemes and arrangements appeal to them.  We can then discuss about symmetry, graph coloring and more.

It would also be interesting to see which color schemes people like, even before the workshop, so here goes!

If you're studying undergrad math, physics or chemistry, chances are you've heard of this thing called a "Group" that is studied in "Group Theory". What is it and why is it so important? I'll explain in a simple way.

The most familiar group is our number system; we have a bunch of numbers, and we have this thing called "$+$" which can take two numbers and churn out another number. A group is just a set of objects, and you have one "operation" (usually called "$\ast$" or "$+$", but those are just names) that tells you how to combine objects to produce other objects in that set, subject to a few rules. Why devise such a "strange chasing game" in a set of objects? That's because such systems are omnipresent in a stupendous array of phenomena:

This'll be quick; the only part of the original blog post that I understood comfortably was the brief (and slightly inaccurate) explanation of traditional image compression. It's how image formats like JPEG can reduce the memory space needed by an image file drastically while losing only a bit of quality.

Tao uses the analogy of the game Tomb Raider as a model to give some intuition for the reasons behind the "weird" consequences of quantum mechanics (QM), in particular the so-called "many worlds interpretation". The game consists of two worlds:

• Internal System: Lara Croft, the protagonist, needs to navigate tombs and solve the puzzles in them to survive. Suppose that she is intelligent and independent of the Player of the game.
• External System: the Player of the game can view the game world and "save" the game to "restore" it when Lara dies. "Restoring" resets Lara's memory (well, she simply went back to an "earlier state", right?). Unfortunately, he cannot see inside the tombs, which limits his assistance.

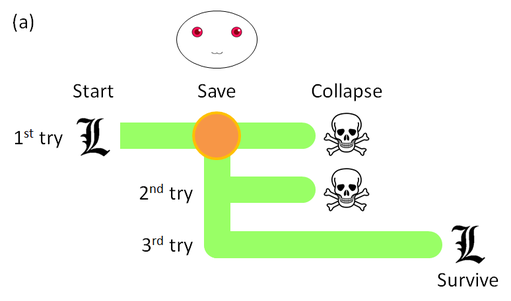
(At this point, Tao apologizes for the violent analogy. Well, I've added a little drama... and fixed a loophole.)

Each save point before a lethal puzzle causes Lara's world (from her point of view) to split into many possible "developments",  some of which involve her failure to solve the puzzle and thus death, while others have her survive. Figure 1 illustrates a sample puzzle: A tomb whose only exit a wooden trapdoor on the floor that leads to an underground passage. The tomb will collapse in, say, five minutes, and Lara ("L") must escape through the passageway, but the trapdoor is locked. The Player (smiley face) helps by creating a save point.

I'm completely unfamiliar with art, but I've had this interesting thought lately. First of all,

(Statement 1)

There are many ways how an art piece can be more than its constituents. The visual arts give a few easy examples, where emotion can be injected into a medium (the "sum of its parts"). The emotion, message, or whatever special qualities that qualify something as art, was not present in the medium itself, yet it present in its final form.

I was proud of this idea, as it was probably the best early research idea I've come up with.

I became very interested in matrices and linear algebra after reading a paper on modelling origami using rotation and translation matrices (Belcastro and Hull, 2012). I began to play with expressing all kinds of things as matrices and seeing what "meanings" matrix operations had in those contexts.

Somehow complex numbers cropped up, and I decided that they were a good candidate for this "interpretation" because multiplying by a complex number meant a rotation and dilation of the complex plane - or an "amplitwist" (Needham, 1996). So I represented a complex number as a rotation matrix together with a scaling factor.

Given a complex number $z = r\mathrm{e}^{\mathrm{i}\theta}$, let $\mathbf{Z} = r\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}.$ Some interesting properties follow immediately from this correspondence:

Another old idea. Given a $2 \times 2$ matrix $\mathbf{A}$,

$$\det(\mathbf{A}) = \begin{bmatrix}1&0\end{bmatrix}\mathbf{A}^T\begin{bmatrix}0&1\\-1&0\end{bmatrix}\mathbf{A}\begin{bmatrix}0\\1\end{bmatrix}.$$
Prove this and extend it to general $n \times n$ matrices. Can you go further than that?