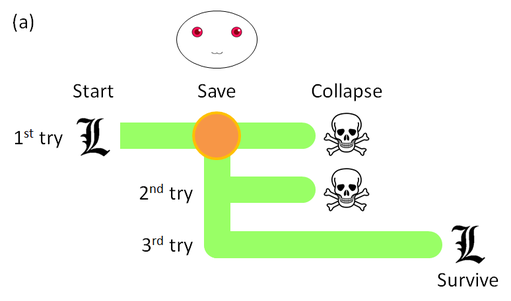
[1.1] Quantum mechanics and Tomb RaiderTao uses the analogy of the game Tomb Raider as a model to give some intuition for the reasons behind the "weird" consequences of quantum mechanics (QM), in particular the so-called "many worlds interpretation". The game consists of two worlds:
(At this point, Tao apologizes for the violent analogy. Well, I've added a little drama... and fixed a loophole.) Each save point before a lethal puzzle causes Lara's world (from her point of view) to split into many possible "developments", some of which involve her failure to solve the puzzle and thus death, while others have her survive. Figure 1 illustrates a sample puzzle: A tomb whose only exit a wooden trapdoor on the floor that leads to an underground passage. The tomb will collapse in, say, five minutes, and Lara ("L") must escape through the passageway, but the trapdoor is locked. The Player (smiley face) helps by creating a save point.  Figure 1(a): Playing out a puzzle in a cave. The Player (smiley face) creates a save point to give Lara Croft ("L") three attempts to clear the puzzle; she only survives the last attempt.
0 Comments
Is it possible to do mathematics WITHOUT background knowledge?... Is it humanly possible to do mathematics on own without research or is the information content too much to discover identities, or methods of proofs on one's own?... But, how to get started then? How to discover mathematics on my own? I wouldn't say that I've been "discovering mathematics", but I definitely have been playing around with many of my original math research ideas, some of which I am happy with. So I introspected a little about my amateur math explorations and how my experience can help people who ask this question. Here is my slightly edited response.  Playful construction is fundamental to research. I'm completely unfamiliar with art, but I've had this interesting thought lately. First of all, Art is more than the sum of its parts. (Statement 1) There are many ways how an art piece can be more than its constituents. The visual arts give a few easy examples, where emotion can be injected into a medium (the "sum of its parts"). The emotion, message, or whatever special qualities that qualify something as art, was not present in the medium itself, yet it present in its final form.  A painting is more than colors on a canvas. I was proud of this idea, as it was probably the best early research idea I've come up with.
I became very interested in matrices and linear algebra after reading a paper on modelling origami using rotation and translation matrices (Belcastro and Hull, 2012). I began to play with expressing all kinds of things as matrices and seeing what "meanings" matrix operations had in those contexts. Somehow complex numbers cropped up, and I decided that they were a good candidate for this "interpretation" because multiplying by a complex number meant a rotation and dilation of the complex plane - or an "amplitwist" (Needham, 1996). So I represented a complex number as a rotation matrix together with a scaling factor. Given a complex number $z = r\mathrm{e}^{\mathrm{i}\theta}$, let $\mathbf{Z} = r\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}.$ Some interesting properties follow immediately from this correspondence: Another old idea. Given a $2 \times 2$ matrix $\mathbf{A}$,
$$\det(\mathbf{A}) = \begin{bmatrix}1&0\end{bmatrix}\mathbf{A}^T\begin{bmatrix}0&1\\-1&0\end{bmatrix}\mathbf{A}\begin{bmatrix}0\\1\end{bmatrix}.$$ Prove this and extend it to general $n \times n$ matrices. Can you go further than that? |
Archives
December 2020
Categories
All
|
RSS Feed